One of the easiest and best-known controllers is the Proportional-Integral-Derivative (PID) controller, where more than half the industrial controllers in use today utilize PID controllers or modified PID control schemes.

This controller has gained its popularity and wide acceptance in the industrial applications due to several advantages:

• ability to compensate most practical industrial processes.
• general applicability to most control systems, especially when the mathematical models of the plants are unknown or when such models are difficult to obtain and thus, analytical approach of designing the controllers will be impossible.
• PID controllers are usually adjusted on site using different types of tuning rules and thus, using these delicate and fine tunings, the accuracy of these controllers will be increased as they are exposed to the practical plant's situations.
• automatic tuning methods and on-line automatic tuning capabilities have further enhanced the accuracy of these controllers.

This controller does have some disadvantages as well:

• does not handle dead times and large non-linearities.
• suitable for single input and single output (SISO) systems only.

In designing this controller, one has to understand the individual components of the controller, that is the Proportional (P), Integral (I) and Derivative (D), and how the individual gains, Kp, KI and KD have to be designed such that the performances of the system meet the specifications.

• P-action: provides and action that depends on the instantaneous value of the control error. It can be used to improve the speed of the system's response and the steady-state error but with limited performance.
• I-action: gives a controller output that is proportional to the accumulated error. It is a slow reaction control mode and is usually used to achieve zero-steady error in the presence of a step reference and/or disturbance.
• D-action: acts on the changing rate of the control error.

The PID controller is usually designed with the general ideal of first satisfying the steady-state errors specification. Thereafter, the desired damping ratio ζ, un-damped natural frequency ωn and/or p, which is usually taken as p>10 ζωn, can then be determined by comparing the plant's transfer function with that of the standard system, such as a standard third-order system, (s+p)(s^2+2ζωns+ωn^2).

With the tuning capability of the PID controllers, it helps to further enhance the accuracy of these controllers in reacting to the practical plant's performances. Controller tuning is the process of selecting the controller parameters, Kp, Ti and Td, to meet given performance specifications. Rules for tuning the PID controllers were based on experimental step responses. One such famous rule is the Ziegler-Nichols rule for tuning PID controllers. This rule helps to suggest a set of values if Kp, Ti and Td based on the transient response characteristics of a given plant that will give a stable operation of the plant. Hence, they often form the basis for tuning procedures used by the manufacturers and process industry.

There are two classical methods for determining the parameters of PID controllers when applying Ziegler-Nichol rules and they are the Step Response method and the Frequency Response method. In the Step Response method, the response of the plant to a unit-step input is obtained experimentally where the PID parameters were chosen acoording to:

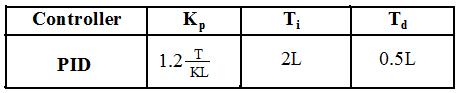
In the Frequency Response method, Ti is set to infinity and Td is set to zero, thus the plant is only under the Proportional control (P-control). In this case, the PID parameters were then chosen according to: